Optimization of the reinforcement schedule
The quantities estimates of the previous chapter are based upon the theoretical rebar lengths as provided by the software. Since the reinforcement bars have specific lengths, usually 12 ή 14 m, ordering them with their exact lengths will lead to the formation of oddments i.e. short rebars of length e.g. 0.80m, which cannot be used. Every reinforcement supplier has his own method to manage these oddments in order to minimize their cost and at the same time offer constructional accuracy. The methods followed in order to manage the issues of oddments and constructional accuracy are generally referred to as optimization. The persons responsible for the reinforcement’s optimization can be either the designer engineer in charge of the detailing or the quantity surveyors of the reinforcement supplier. The following paragraphs present generally the issue of optimization together with a proposition.
In every case, no matter which optimization method is being followed, the estimates1 of the bars number used in the reinforcement implementation must mention the percentage of rebar losses2. This happens because the reinforcement cost estimation3 must include these losses as well.
The Engineer makes the reinforcement schedules based upon two basic assumptions:
1st) by presuming that the formworks will be constructed exactly as shown in the drawings and
2nd) Based upon the dimensions of the drawings and the theoretical anchorage and lap-splice lengths, he/she defines the theoretical rebar lengths.
However, in the construction, the dimensions of the real formworks present an unintended ‘constructional deviation’; as a result, cutting rebars to their theoretical lengths is economically challenging and creates a large amount of oddments.
The unavoidable constructional deviation depends upon the tools, the experience and the dili- gence of the contractor responsible for the formworks’ implementation. This deviation is consid- ered to be in the order of 1 up to 3cm.
Moreover, the rebars’ cut to random lengths is productive only in the case of coil-cutting ma- chines but even in these cases the coil usually covers rebars with a diameter up to Φ12, or Φ14. In all other cases, the rebar must be cut to supplementary amounts of industrial bars with usual lengths equal to 12 or 14m. In order for this to be feasible, and always to a certain degree, the available rebar oddments must be separated according to their diameter and length which from a practical point of view, is a complex and space/labor demanding procedure.
Finally, there will always be rebar losses. A large amount of losses includes an increased mate- rial cost and a lower labor cost while a small amount of losses corresponds to a larger labor cost. The targeted goal is the optimum combination that leads to an economical solution where the minimum rebars length requirements are obligatorily met.
An effective optimization method which provides an effective combination of cost-losses is the method of the ‘standardized cut and storage’ in which the rebars have length of a specific step equal to e.g. 25cm 4.

1 The theoretical mass of the rebars mentioned in table 1 (e.g. for Φ20, 2.47 kg/m) usually in practice, has a deviation that ranges from +1 to
+2%.
2 The loss percentage is a relative quantity and is completely independent of the actual mass. It varies from +1% to +6%, according to the optimization method followed by each reinforcement supplier.
3 The most simple and practical way to include the reinforcement in a bid and to estimate its cost, is by setting the price based upon the actual mass of the properly shaped and ready-to-implement reinforcement, having calculated the losses as well. Each total amount will be defined by measuring the reinforcement’s weight.
4 The standardized cut and storage offers many advantages to the organized reinforcement suppliers. The two major advantages are:
The following paragraphs examine 3 optimization examples regarding the rebars of specific structural elements, based upon the following assumptions: (a) constructional deviation= 2cm and (b) standardized cut with a step equal to = 0.25m.
 1st example (the slab of §3.5.1)
1st example (the slab of §3.5.1)
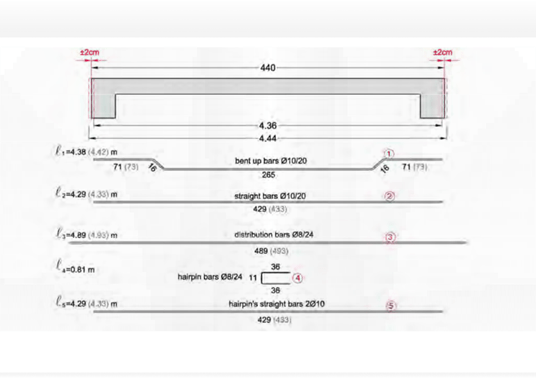
In the example of the one-way slab in §3.5.1 the total slab length was 4.40m and the length of the lower rebars was 4.33m.
In both ends of the slab, the side formwork might slip to the left or to the right around 2cm there- fore, in the two worst cases, the slab’s span length may take a value between 4.40-0.02- 0.02=4.36m and 4.40+0.02+0.02=4.44m. Rebars are critically affected when the slipping of the slab’s ends happens towards the inside. In order to avoid such a case and have the proper cov- er depth, the lower rebars must be formed with a length equal to 4.33-0.02-0.02=4.29m.
The standardized cut length is 4.25m or 4.50m. In this case, it is not possible to cut the rebar to a length either shorter (than 4.25m) or longer (than 4.50m) and therefore the optimization re- gards only the constructional deviation. Consequently, the rebars (2) must be cut to a length of l2=4.29m instead of 4.33m. The same thing applies and to rebars (5) which will be cut to a length equal to l5=4.29m rather than 4.33m.
By an analogous way of thinking, we concluded that the rebars (1) will have a cut-length of l1=4.38m instead of 4.42m. The length difference is divided in the upper horizontal parts of the bent-up rebars which will be formed with a length equal to 71cm rather than 73cm.
The hairpin rebars (4) have a short length and there is no reason for cut optimization. The rebars (3) will have a cut-length of l3=4.89m rather than 4.93m.

- The rebars’ cut and storage as well as the gathering of the rebars requested by an order, are separate tasks performed by different person- nel.
- at all times, the supplier may know the exact number of every specific length-rebar requested by e.g. the daily orders, and therefore he can manage his stock. The ‘standardized cut and storage’ entails losses in the order of +2%.
 2nd example (the two slabs of §3.5.3)
2nd example (the two slabs of §3.5.3)
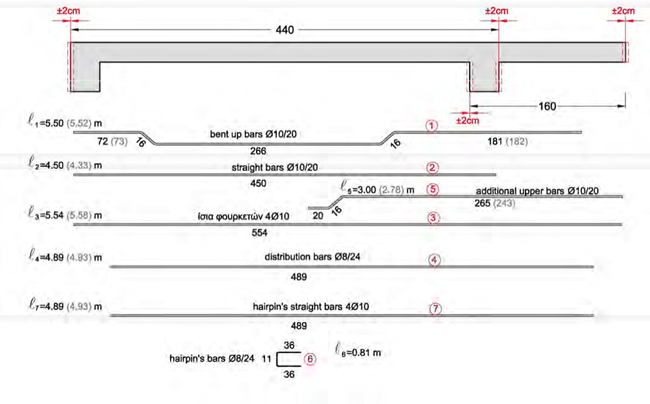
In the example of the simply supported slab connected with a cantilever slab mentioned in
§3.5.3, the total length of the first slab was 4.40m and of the second slab was 1.60m. According to the previous example the total lengths of those two slabs may range between 4.36 and 4.44 for the first slab and between 1.56 and 1.64 for the second slab.
The effect of ‘constructional deviation’ upon the optimization:
The constructional deviation of the two slabs does not affect the majority of the rebars’ lengths because it is possible for the latter to move to the adjacent slabs. Rebars (3) are the only ones that have limitation and since they do not have a margin either to the left or to the right, they must be formed with a length equal of 5.54m instead of 5.58m. For the same reason the vertical bars (4) and (7) must be formed with a length equal to 4.89m rather than 4.93m.
The effect of ‘standardized cut’ upon the optimization:
The rebars(1) must have a length of 5.50m instead of 5.52m due to a minor difference (where the left upper horizontal part of the bent-up rebar becomes 72cm instead of 73cm and the right upper horizontal part becomes 181cm instead of 182cm).
The rebars (2) will be formed with a length equal to 4.50 rather than 4.33.
The rebars (5) will be 3.00m long instead of 2.78 (where the last length will become 2.65 in- stead of 2.43)
The rest of the rebars have a limitation and cannot be standardized therefore, the bars (4) and
(7) will be formed with a length equal to 4.89 rather than 4.93.
 3rd example (the beam of § 3.4.1)
3rd example (the beam of § 3.4.1)

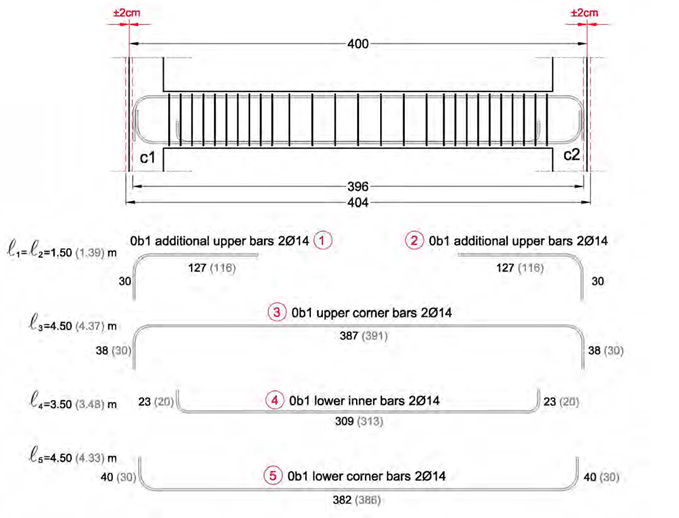
In the example of the simply supported beam in § 3.4.1 the beams is 4.00m long and therefore, the total length may vary between 3.96m and 4.04m. The constructional deviation does not af- fect the support rebars (1) and (2), which will be formed with a total length equal to 1.50m in- stead of 1.39 (where the last length will become 1.27 rather than 1.16).
The lower and upper rebars of the beam are affected by the constructional deviation. This is the reason why the bars length must be shortened by 4cm, however, the hooks may become larger so as to achieve the required final length (hooks must not extend outside the concrete’s mass and inside the beam’s cover depth).
The rebars (3) will have a total length of 4.50m instead of 4.37l, with a span length equal to 3.87 rather than 3.91 and their hooks will be 0.38 long instead of 0.30.
Consequently the reinforcement bars (4) will have a total length equal to 3.50m rather than 3.48, with span length 3.09 instead of 3.13 and their hooks will be 0.23 long rather than 0.20.
The rebars (5) will have a total length of 4.50m instead of 4.33, with span length equal to 3.82 rather than 3.86 and their hooks will be 0.40 long instead of 0.30.