Design Principles of Concrete Structures
Lecture 6
Under Reinforced & Over Reinforced
(Derivation)
Under-Reinforced Failure
Stage-I, Un-cracked Section
N.A. position is fixed, means “la” remains constant. Only “T” and “Cc” increase with the increase of load
Stage-II, Cracked Section
When section cracks, N.A. moves towards compression face means “la” increases. “T” and “Cc” also increase.
a/2 Cc

Internal Force Diagram
Under-Reinforced Failure (contd…)
Stage-III, Yielding in Steel Occur
T = As fy remains constant and Cc also remains constant. “la” increases as the
N.A. moves towards compression face because cracking continues.
Failure initiates by the yielding of steel but final failure is still by crushing of concret.

Und er-Reinforced Failure( contd…).
Derivation for p
Design Moment Capacity
For tension controlled section <D = 0..9
And
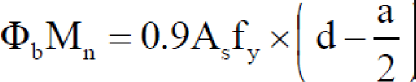
Under–Reinforced Failure (contd.,.. “‘ ,. )
Put value of
a from (1) to (2)
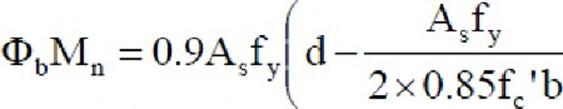

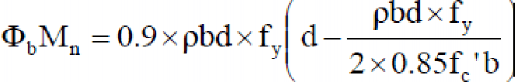
For econon1ical Design
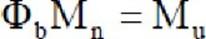

By Simplifaication

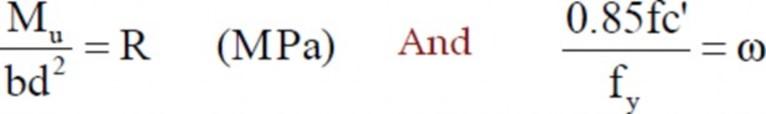

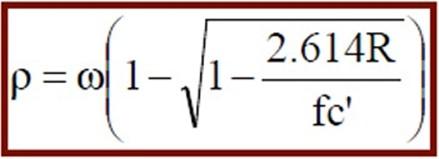
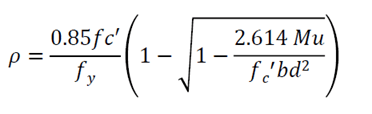
As we know, Reinforcement Ratio is,
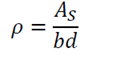
So,
Area of Steel As will be
𝐴𝑠 = 𝜌 × 𝑏𝑑
Trial Method for the determination of “As”
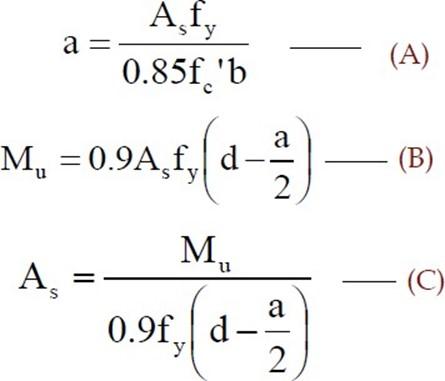
Trial # 1, Assume some value of “a” e.g. d/3 or d/4 or any other reasonable value, and put in (C) to get “As”
Trial # 2, Put the calculated value of “As” in
-
to get “a”. Put this “a” value in (C) to get
“As”
Keep on doing the trials unless “As” from a specific trial becomes equal to the “As” calculated from previous trial.
THIS VALUE OF AS WILL BE THE FINAL ANSWER.
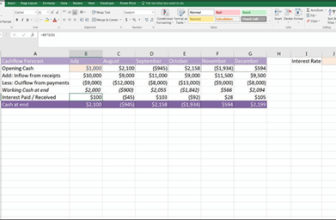
Is The Section is Under-Reinforced or NOT?
- Calculate ρ and if it is less than ρmax, section is under reinforced
- Using “a” and “d” calculate εt if it is ≥ 0.005, section is under-reinforced (tension controlled)
- If section is over-reinforced than in the following equation –ve term will appear in the under-root.
- Calculate ρ and if it is less than ρmax, section is under reinforced
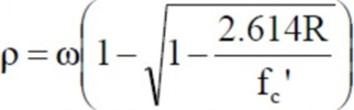
 Over-Reinforced Failure
Over-Reinforced Failure
Stage-I, Un-cracked Section
Stage-II, Cracked Section
These two stages are same as in under-reinforced section.
Stage-III, Concrete reaches strain of
0.003 but steel not yielding
We never prefer to design a beam as over- reinforced (compression controlled) as it will show sudden failure.
Φ = 0.65 εs < εy fs<fy
Stage-III, Concrete reaches strain of 1 0.0103 but steel not yielding (co11td )


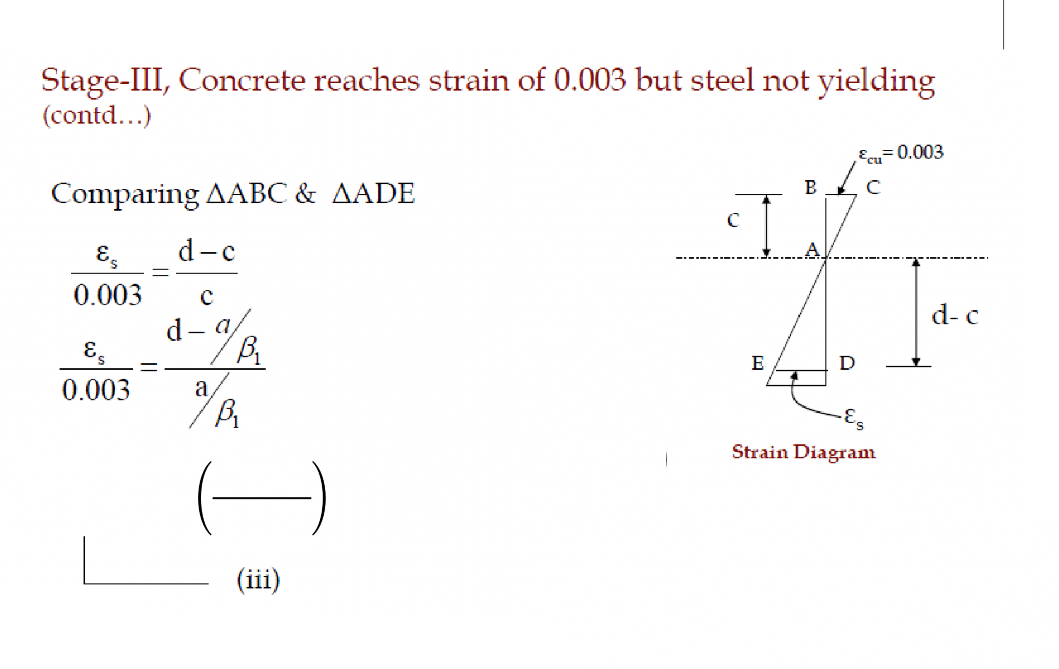
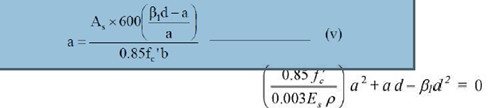
Stage–III, Concrete reaches strain of 0.003 but steel not yielding(contd…)
Putting value of fs from (iv ) to (ii)
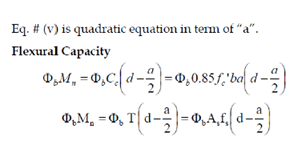
Summary

Concluded