Design Principles of Concrete Structures
Lecture 12
T & L Beams
T & L Beams
T & L Beams
- With the exception of pre-cast systems, reinforced concrete floors, roofs, decks, etc., are almost always kept monolith.
-
Beam stirrups and bent bars extend up into the slab.
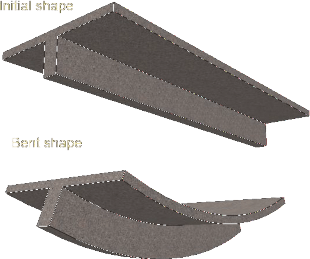
- It is evident, therefore, that a part of the slab will act with the upper part of the beam to resist longitudinal compression.
- The slab forms the beam flange, while a part of the beam projecting below of the slab forms is called the “web” or “stem”.
T & L Beams (contd…)
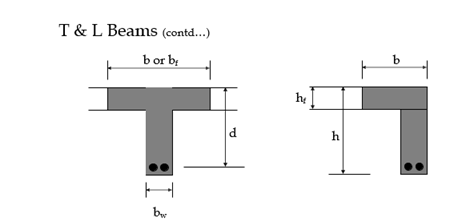
b = Effective width
bw = width of web/rib/stem
hf = Thickness of flange
Effective With of T & L Beams
T-Beams
Effective width will be minimum of the following:
1. L/4
2. 16hf + bw
3. bw + ½ x (clear spacing of beams (Si) on both sides) = c/c spacing for beams at regular interval
Effective With of T & L Beams
L-Beams
Effective width will be minimum of the following:
- L/12
- 6hf + bw
- bw + Si/2 on one side
Note: Only above discussion is different for isolated (pre- cast) T or L beam. Other discussion is same (analysis and design formula).
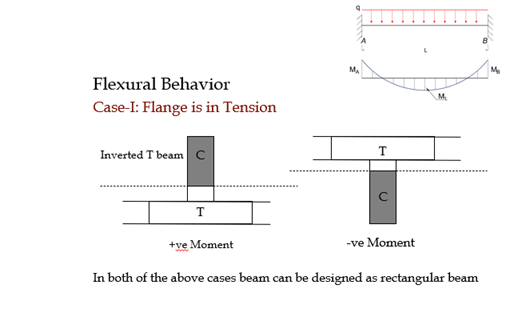
Flexural Behavior (contd…)
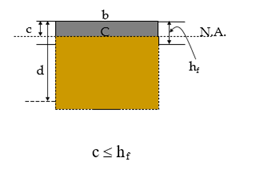
Case-II: Flange is in Compression and N.A. lies with in Flange
beam can be designed as a rectangular beam hf of total width “b” and d effective depth “d”.
Flexural Behavior (contd…)
Case-III: Flange is in Compression and N.A. lies out of the Flange
Beam has to be designed as a T-Beam.
Separate expressions are to be developed for analysis and design.
b
Flexural Behavior (contd…)
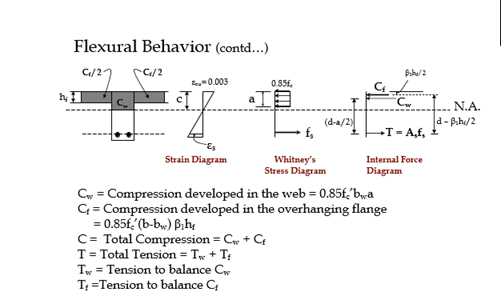
It is convenient to divide total tensile steel into two parts. The first part, Asf represents the steel area which, when stressed to fy, is required to balance the longitudinal compressive force in the overhanging portions of the flange that are stressed uniformly at 0.85fc’.
The remaining steel area As – Asf, at a stress fy, is balanced by the compression in the rectangular portion web above the N.A.
Tf = Asf fs
Tw = Aswfs= (As–Asf)fs
Flexural Behavior (contd…)
Majority of T and L beams are under-reinforced (tension controlled). Because of the large compressive concrete area provided by the flange.
For longitudinal equilibrium
SF = 0
Tf = Cf& Tw = Cw

Flexural Behavior (contd…)
Flexural Capacity
From Compression Side
Mn = Mnf + Mnw

Flexural Behavior (contd…)
Flexural Capacity
From Tension Side
Mn = Mnf + Mnw

Tension Controlled Failure of T-Beam

Tension Controlled Failure of T-Beam (contd…)
For longitudinal equilibrium
T = C w + Cf
T = C w + Tf
A s f y = 0.85fc ‘ b w a + A sf f y
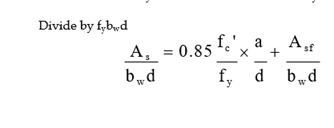

Concluded