Design Principles of Concrete Structures
Lecture 11
Doubly Beams
Doubly Reinforced Beams
“Beams having both tension and compression reinforcement to allow the depth of beam to be lesser than minimum depth for singly reinforced beam”
- By using lesser depth the lever arm reduces and to develop the same force more area of steel is required, so solution is costly.
- Ductility will be increased by providing compression steel.
-
Hanger bars can also be used as compression steel reducing the cost up to certain cost.
Doubly Reinforced Beams (contd…)
-
For high rise buildings the extra cost of the shallow deep beams is offset by saving due to less story height.
- Compression steel may reduce creep and shrinkage of concrete and thus reducing long term deflection.
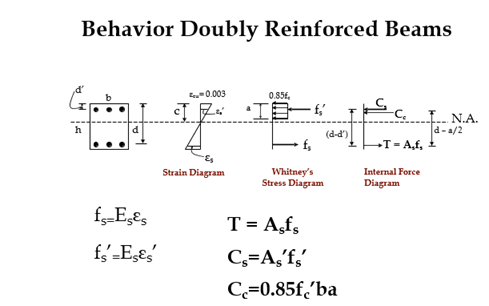
Behavior Doubly Reinforced Beams
Tension steel always yields in D.R.B. There are two possible cases:
- Case-I Compression steel is yielding at ultimate condition.
- Case-II Compression steel is NOT yielding at ultimate condition.

Behavior Doubly Reinforced Beams (contd…)
Case-I Both Tension & Compression steel are yielding at ultimate condition
fs = fy and fs’=fy
Location of N.A.
Consider equilibrium of forces in longitudinal direction
T = Cc + Cs
Asfy = 0.85fc ‘ ba + Afy
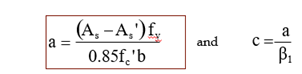

Case-I Both Tension & Compression steel are yielding at ultimate condition (contd…)
T = total tensile force in the steel
T=T1 +T2
T1 is balanced by Cs T2 is balanced by Cc
T1 = Cs
2
T2 = Cc
Case-I Both Tension & Compression steel are yielding at ultimate
condition (contd…)
Moment Capacity by Compression Steel
Mn1=Cs(d–d’)=As‘fy(d–d’)
=T1(d–d’)=As
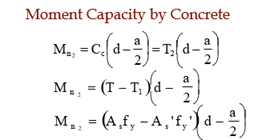
Case-I Both Tension & Compression steel are yielding at ultimate condition (contd…)
Total Moment Capacity
Mn = Mn + Mn2
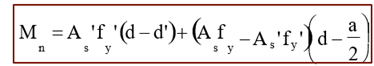

Example No. 1
Example:
A doubly reinforced section has the following sectional properties:
As’ = 570 mm2
d’ = 60 mm
fy = 300 MPa
As = 3042 mm2 b = 300 mm
Calculate ΦbMn for the following two cases:
fc’ = 20 MPa d = 525 mm
fc’ = 35 MPa d = 225 mm
Example No. 2
Example:
Design a simply supported rectangular beam having a span of 6m, subjected to a total factored load (including self-weight) of 70 kN/m. The depth of beam is not to exceed span/12 and width is 300m.
fc’ = 20 MPa, fy = 420 MPa Design for following two cases:
-
As‘ is to be as small as possible

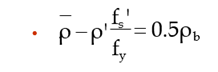
Concluded